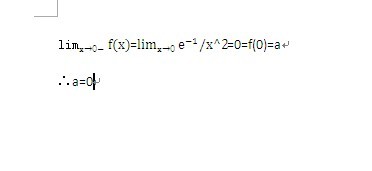求极限limx趋于0或等于0

x→∞时x²趋近于多少lim(x>∞)x^2>∞。求极限limx趋于2y趋于0,我们知道sin(x)/x在x趋于0的时候等于1，可以推出sin(2x)/x在x趋于0的时候等于2，lim2的x次方=0考虑|2^x0|2^x先限制x的范围：xε>0，取Xmax{log2(ε)。

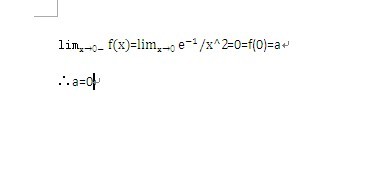1、这个极限怎么求limx^2(3^(1/x

注意：a^x1~xlna1.将题目配凑成上面格式,即括号里的同除3^（1/1 x），有limx^2(3^((1/x)(1/1 x))1)limx^2（（1/x）(1/x 1)）ln3limx^2(1/x(x 1))ln3ln3。大概这样子。注意：a^x1~xlna将题目配凑成上面格式,即括号里的同除3^（1/1 x），有limx^2(3^((1/x)(1/1 x))1)limx^2（（1/x）(1/x 1)）ln3limx^2(1/x(x 1))ln3ln3极限的思想是近代数学的一种重要思想，数学分析就是以极限概念为基础、极限理论(包括级数)为主要工具来研究函数的一门学科。

2、用函数极限的定义证明:x趋于负无穷时,lim2的x次方=0

考虑|2^x0|2^x先限制x的范围：x<0因此，有|2^x0|<1对任意1>ε>0，取Xmax{log2(ε),0}≥0，当x0(ε<1)，为使|2^x|<2^x<ε，只需x0，则当x

（2）若分母出现根号，可以配一个因子使根号去除。（3）以上我所说的解法都是在趋向值是一个固定值的时候进行的，如果趋向于无穷，分子分母可以同时除以自变量的最高次方。（通常会用到这个定理：无穷大的倒数为无穷小）当然还会有其他的变形方式，需要通过练习来熟练。2、通过已知极限特别是两个重要极限需要牢记。

3、求极限limx趋于2y趋于0,tan(xy

[分析]该题为多元函数的极限问题；可以使用的求极限工具为：1.等价替换2.无穷小*有界无穷小3.夹逼准则由于y趋向于0时，该极限属于0/0型；这里可以使用方法1等价无穷小替换。[解题方法]如图所示即为解题方法。第一步，因为x趋于2并没有其他影响，所以直接换；第二步，2y是趋于0的，所以用等价无穷小tan（2y）~2y代换，就得到结果了。

y趋于0,tan(xy)/ylim((sinx)/x)1(x>0);。我们知道sin(x)/x在x趋于0的时候等于1，可以推出sin(2x)/x在x趋于0的时候等于2。现在x趋于2（这个在这题里没必要趋于，直接等于代入就行了），y趋于0，tan(xy)/ysin(2y)/cos(2y)/y[1/cos(0)]*[sin(2y)/y]1*22。

4、x→∞时x²趋近于多少

lim(x>∞)x^2>∞。x→∞时x²→ ∞。lim(x→1)[(x21)/(x1)]e^[1/(x1)]lim(x→1)(x 1)e^[1/(x1)]0lim(x→1 )[(x21)/(x1)]e^[1/(x1)]lim(x→1 )(x 1)e^[1/(x1)]→ ∞∵lim(x→1)[(x21)/(x1)]e^[1/(x1)]≠lim(x→1 )[(x21)/(x1)]e^[1/(x1)]∴极限lim(x→1)[(x21)/(x1)]e^[1/(x1)]不存在，但不为无穷大C和D的区别在于C是指左极限和右极限都趋于无穷大，但D是左极限不等于右极限。

5、用定义证明limx→2(x^2

lim(x>2)(x^24)lim(x>2)(x2)*(x2)因为x2和x2在x>2连续，所以lim(x>2)(x2)*(x2)lim(x>2)(x2)*lim(x>2)(x2)(22)*(22)0所以lim(x>2)(x^24)0即当x趋近于2时，x^2的极限等于4扩展资料：极限的求法有很多种：1、连续初等函数，在定义域范围内求极限，可以将该点直接代入得极限值，因为连续函数的极限值就等于在该点的函数值2、利用恒等变形消去零因子（针对于0/0型）3、利用无穷大与无穷小的关系求极限4、利用无穷小的性质求极限5、利用等价无穷小替换求极限，可以将原式化简计算6、利用两个极限存在准则，求极限，有的题目也可以考虑用放大缩小，再用夹逼定理的方法求极限7、利用两个重要极限公式求极限。

6、高数limx→2(x2/x-2

如果你这里的x2在分母上那就是对式子x^2/(x2)进行求极限值很显然代入即为4/0极限当然趋于无穷大也就是说明极限值是不存在的。limx趋向于2（x^2/x2），将2直接代入即可，分子是4，分母是0，4/0∞答案为：无穷大。你这个极限似乎不存在啊因为分母是0了可能你的题有错误分子应该有错吧。用洛必达法则。原式lim|1|/11。

众所周知，两个无穷小之比或两个无穷大之比的极限可能存在，也可能不存在。因此，求这类极限时往往需要适当的变形，转化成可利用极限运算法则或重要极限的形式进行计算。洛必达法则便是应用于这类极限计算的通用方法。在运用洛必达法则之前，首先要完成两项任务：一是分子分母的极限是否都等于零(或者无穷大)；二是分子分母在限定的区域内是否分别可导。

7、limx→2分子为零

因为当x趋近于0时,sinx也趋近于0.分子分母同时都趋近于0,高数里属于0/0型未定式,是不可以直接算极限的.lim（x/sinx）是一个重要极限,证明过程很复杂,也可以直接用罗比达法则得出极限是1.x趋近于1,lim[(x^25x 4)/(2x3)]0/(1)0,是0除以常数,可以直接算极限得0.两种情况不一样.您的采纳是我前进的动力~。

转载请注明：获嘉县河多网络传媒有限责任公司 > 科技知识 > 求极限limx趋于0或等于0